Farbtiefe bei Film-Scannern und Bilddateien

Was versteht man eigentlich unter dem Begriff Farbtiefe? Was bedeutet es, wenn ein Scanner eine Farbtiefe von 42 Bit hat, die entsprechenden Scans jedoch als 48 Bit Dateien abspeichert? Warum liefert ein Scanner mit 48 Bit Farbtiefe bei Schwarz-Weiß-Bildern nur 8 oder 16 Bit Farbtiefe? Wie viele Farben sind überhaupt bei einer Farbtiefe von 24 Bit darstellbar bzw. unterscheidbar?

Und warum hat ein CMYK-Bild weniger Farben als das entsprechende RGB-Bild obwohl es 32 Bit anstatt 24 Bit hat? Liefert ein Scanner mit 48 Bit Farbtiefe wesentlich bessere Bilder als einer mit nur 36 Bit Farbtiefe? Sollte man seine Scans immer mit der maximalen Farbtiefe durchführen und speichern um bestmögliche Ergebnisse zu erzielen? Was ist der Dichteumfang oder Dynamikumfang eines Scanners, etwa dasselbe wie die Farbtiefe? Fragen über Fragen, rund um ein einziges Thema. Die Liste der Fragen lässt sich wohl ewig fortsetzen; Grund genug für mich, dieses Thema einmal ausführlich zu durchleuchten und anhand von einfachen Beispielen zu erklären.

In den folgenden Unterkapiteln verwende ich immer dasselbe Bild, um die Unterschiede zwischen den einzelnen Farbtiefen und Modi zu sehen. Hier oben erscheint das Matterhorn ein erstes Mal, und zwar so wie das Bild ursprünglich gemacht wurde. Natürlich muss man bei diesem und auch bei den folgenden Bildern berücksichtigen, dass die Bilder fürs Web optimiert und stark komprimiert wurden um die Ladezeit dieser Seite in Grenzen zu halten.

Erklärung des Begriffs Farbtiefe

Ein Bild besteht bekanntlich aus vielen einzelnen Bildpunkten. Unser Bild vom Matterhorn hat zum Beispiel 300 einzelne Pixel in jeder Zeile. Insgesamt gibt es 200 Zeilen, so dass unser Bild eine Auflösung von 300 x 200 Pixeln hat. Unser Bild besteht also aus 60.000 einzelnen Bildpunkten.

Jeder einzelne Punkt des Bildes kann eine eigene Farbe haben. Bei einem einfachen Schwarz/Weiß-Bild gibt es für jeden Bildpunkt entweder den Zustand schwarz oder weiß. In einem einzigen Bit (Inhalt Null oder Eins) kann also für einen Bildpunkt gespeichert werden, welche Farbe der Pixel hat. Man spricht deshalb von einer Farbtiefe von 1.

Je mehr Bits man für einen einzelnen Bildpunkt zur Verfügung hat desto mehr Farbtöne können für den Pixel unterschieden werden; Reserviert man für jeden Pixel 8 Bit im Speicher, so können 2⁸ = 256 Farbtöne dargestellt werden. Bei einem normalen Farbbild mit einer Farbtiefe von 24 Bit können demnach 2²⁴ Farbtöne unterschieden werden. Das sind ca. 16.7 Millionen Farbtöne.

Unter dem Begriff Farbtiefe versteht man die Anzahl der pro Pixel zur Verfügung stehenden Bits zur Speicherung der Farbinformationen. Die Anzahl der möglichen Farbtöne berechnet sich wie folgt: N_Farbtöne = 2^Farbtiefe

Schwarz/Weiß-Bilder mit 1 Bit Farbtiefe, Rasterbilder

Bevor wir zu Farbbildern mit vielen bunten Farben kommen tasten wir uns an den Begriff Farbtiefe langsam heran, indem wir mit dem einfachsten erdenkbaren Farbmodus beginnen, nämlich einem Schwarz/Weiß-Bild mit einer Farbtiefe von 1 Bit. Gemäß obiger Formel lassen sich bei einer Farbtiefe von 1 Bit also genau 2¹ = 2 Farbtöne unterscheiden. Ein Pixel ist entweder schwarz oder weiß.

Solche Bilder findet man im Bereich der Fotographie selten vor. Reine Schwarz-Weiß-Bilder findet man eher im Bereich der Konstruktion. Und natürlich entsteht eine normale Buch- oder Zeitungsseite aus einem Schwarz/Weiß-Druck mit 1 Bit Farbtiefe, also entweder schwarz oder weiß. Unser Bild vom Matterhorn zeigt nur schemenhaft die Umrisse des Gipfels. Die Bäume und Sträucher können gegenüber dem Hintergrund nicht differenziert werden.

Wie schaffen es jedoch schwarz/weiße Tageszeitungen aussagekräftige Bilder abzudrucken? Schließlich gilt doch auch hier das Prinzip, dass ein Pixel entweder schwarz oder weiß ist. Das Geheimnis liegt in einem Verfahren, das als Rasterung bezeichnet wird. Betrachtet man in unserem gerasterten Matterhorn-Bild die linke obere Ecke mit der Lupe so erkennt man, dass genau jeder zweite Pixel schwarz ist, und zwar sowohl in horizontaler als auch in vertikaler Richtung. Es entsteht der Eindruck eines mittleren Grautones. Betrachten wir die rechte Flanke des Gipfels wo viel Schnee liegt: Wir erkennen, dass einige wenige schwarze Pixel das helle Weiß etwas abdunkeln. Im Gegensatz dazu erkennen wir bei den Bäumen und Sträuchern im Vordergrund, dass einzelne weiße Pixel in den schwarzen Flächen die Bäume etwas aufhellen.

Bei reinen schwarz/weiß-Bildern mit 1 Bit-Farbtiefe lassen sich durch Rastern auf Kosten der Auflösung mehrere Grautöne simulieren.

Wer sehen also, dass selbst bei der niedrigsten erdenkbaren Farbtiefe von 1 Bit durch Rasterung unterschiedliche Farbtöne (Grautöne) dargestellt werden können. Es wird also quasi eine höhere Farbtiefe simuliert; dies geht auf Kosten der Auflösung, denn bei der Rasterung werden mehrere Bildpixel quasi zusammengefasst um durch unterschiedliches Setzen von schwarzen und weißen Punkten mehrere Grautöne zu erzeugen. Die physikalische vertikale Farbtiefe wird also quasi durch eine horizontale Farbtiefe auf Kosten der Auflösung vergrößert. Je höher die Auflösung des Bildes ist desto weniger sticht der Effekt der Rasterung ins Auge. Man teste dies, indem man das gerasterte Matterhorn-Bild aus 2 m Entfernung betrachtet.

Werfen wir abschließend einen Blick auf die Tonwertkurve. Sie besteht wie erwartet lediglich aus zwei Balken, einem ganz hohen schwarzen ganz links und einem etwas niedrigeren weißen ganz rechts.

S/W-Bilder mit 2 Bit Farbtiefe, Verwendung von Paletten

Schwarz/Weiß-Bilder mit einer Farbtiefe von 2 Bit haben zwar in der Praxis keine Bedeutung, jedoch hilft mir dieses Beispiel um die Begriffe Farbtöne und Paletten anschaulich zu erläutern. Gemäß unserer obigen Formel hat ein Bild mit 2 Bit Farbtiefe insgesamt 2² = 4 verschiedene Farbtöne. Bei einem SW-Bild geht die Farbskala also in vier Stufen von schwarz über dunkelgrau und hellgrau zu weiß. Man spricht besser von einer Grauskala als von einer Farbskala.

Das folgende Bild vom Matterhorn wurde mit einer Farbtiefe von 2 Bit abgespeichert. Das gesamte Bild besteht also nur aus 4 Farben, obwohl man dies auf den ersten Blick nicht vermuten würde. Bei näherer Betrachtung kann man jedoch die 4 einzelnen Farbtöne genau voneinander differenzieren. Es ist doch verblüffend welche Aussagekraft ein Bild mit nur 4 Farbtönen bereits erhalten kann, nicht?

Vergleicht man die 4 Farben unseres Matterhorn-Bildes mit den 4 Farben in unserer Grauskala oben, so findet man keine Gemeinsamkeiten. Unsere Grauskala zeigt 4 Graustufen von schwarz bis weiß in gleichmäßigen Schritten. In unserem Foto sind jedoch 4 Graustufen ganz anderer Helligkeit verwendet; schwarz und weiß kommen überhaupt nicht vor; Was hat es damit auf sich?

Die Angabe der Farbtiefe in der Größe 2 Bit sagt nichts über die tatsächlich verwendeten Farben aus. Sie sagt nur aus, dass sich das Bild aus maximal 4 verschiedenen Farbtönen zusammensetzt. Welche Farbtöne dies sind wird in einer sogenannten Farbpalette gespeichert. Man kann sich dies so vorstellen: Ein Maler hat zu Hause in seinem Atelier Hunderte verschiedener Farbtöpfe. Um auf einer Vernissage vor Publikum ein schnelles Bild zu zeichnen mischt er sich aus all seinen Farben einige auf seiner kleinen, transportablen Palette zusammen, die er dann mitnimmt und die er zum Malen des Bildes benötigt.

Die Farbtiefe macht nur eine Angabe zu der Anzahl der Farben nicht zu den tatsächlich vorhandenen Farbtönen. In einer Palette mit 4 Farben können 4 beliebige Farbtöne aus einer großen Palette gespeichert werden.

In unserem obigen Bild mit insgesamt nur 4 Farbtönen stehen die 4 verschiedenen Bit-Kombinationen also nicht für 4 Grautöne in einer linearen Grauskala sondern zeigen auf 4 verschiedene Grau-Farben, deren einzelner Farbton genau in der Farbpalette gespeichert ist. Die Tonwertkurve zeigt die vier verwendeten Grautöne in dem Bild; sie befinden sich alle ziemlich im mittleren Bereich der Grauskala.

Schwarz-Weiß-Bilder mit 4 Bit Farbtiefe

Erhöht man die Farbtiefe von 2 auf 4 Bit, so lassen sich bereits 2⁴ = 16 verschiedene Grautöne darstellen. Unsere lineare Grauskala zeigt die 16 Grauwerte von schwarz bis weiß. Man erkennt, dass sich mit 16 Grautönen bereits ausreichend viele Grautöne darstellen lassen. Vor allem die dunklen Grautöne lassen sich nur schwer vom reinen schwarz unterscheiden.

Unser Bild vom Matterhorn sieht mit 16 Grautönen bereits sehr wirklichkeitsnah aus; Auch hier sei wieder gesagt, dass nicht die 16 Grautöne aus obiger linearer Grauskala verwendet werden sondern dass dem Bild eine Farbpalette mit 16 optimierten Grautönen zugrunde liegt. Ein reines Schwarz und ein reines Weiß kommen in der Grau-Palette nicht vor. Im Tonwertdiagramm erkennt man wie die 16 Grautöne verteilt sind: Die meisten Grautöne konzentrieren sich im Bereich eines mittleren Grautones.

Durch die größere Anzahl von Grautönen wird das Bild nicht nur farbenreicher sondern auch detailreicher. Um dies nachzuvollziehen vergleiche man die Bäume im Vordergrund mit denen auf dem Bild mit 2 Bit Farbtiefe im vorigen Kapitel. Betrachtet man den Himmel, so sind die einzelnen Palettenfarben deutlich voneinanander unterscheidbar. Hier wird klar erkenntlich, dass 16 Grautöne einfach noch nicht ausreichen, um ein Bild ohne störende Farbeffekte wiedergeben zu können.

Schwarz/Weiß-Bilder mit 8 Bit Farbtiefe

Normalerweise werden Schwarz/Weiß-Bilder mit einer Farbtiefe von 8 Bit gescannt und gespeichert; Pro Bildpunkt steht also 1 Byte (8 Bit) zur Verfügung. Das wiederum bedeutet nach unserer obigen Formel, dass pro Bildpunkt 2⁸ = 256 Grautöne zur Verfügung stehen. Unsere lineare Grauskala zeigt einen fließenden Übergang von schwarz bis weiß. Tatsächlich besteht jedoch auch dieser Balken aus 256 einzelnen Vertikalstreifen unterschiedlichen Farbtons, die man bei starker Vergrößerung auch erkennen kann.

Unser Matterhorn-Bild wirkt mit 256 Grautönen natürlich und scharf. Es scheint keine Bildinformation zu fehlen wie in den vorigen Kapiteln. Wenn man bei näherer Betrachtungsweise immer noch leichte Schlieren und Farbsprünge erkennen kann, dann liegt dies an der durchgeführten Komprimierung und Verkleinerung des Bildes, um die Ladezeit dieser Webseite niedrig zu halten.

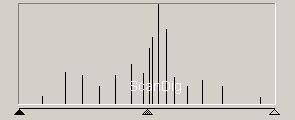
Die Farbpalette dient bei diesem Bild nicht mehr dazu, eine Auswahl von Grautönen aus einer Gesamtauswahl zu speichern, denn der normale Bildschirmwiedergabemodus hat wie das Bild nur eine Farbtiefe von 8 Bit. In der Palette sind demnach die vollen 256 Grautöne von schwarz bis weiß wie in obiger linearen Skala enthalten. Die Tonwertkurve zeigt dies deutlich anhand eines durchgehenden Verlaufes ohne Lücken. Vergleicht man diese Tonwertkurve mit derjenigen im vorigen Kapitel, so erkennt man dieselbe Gipfellinie, allerdings gibt es keine Lücken mehr zwischen den einzelnen Vertikalbalken. Sämtliche 256 Tonwerte sind also in dem Bild vorhanden.

Ein Computer-Bildschirm kann SW-Bilder mit 256 verschiedenen Grautönen darstellen. Das Scannen/Speichern von SW-Bildern mit 8 Bit Farbtiefe entspricht also dem gängigen Datei- und Darstellungsformat von Schwarz/Weiß-Bildern.

Eine höhere Farbtiefe als 8 Bit macht also zur Darstellung von Schwarz/Weiß-Bildern keinen Sinn. Wozu es dennoch Farbtiefen bis 16 Bit bei SW-Bildern gibt, dazu komme ich später.

Bedeutung der Farbtiefe bei Farbbildern

Machen wir nun den Sprung von Schwarz/Weiß-Bildern zu Farbbildern; Alles oben gesagte über Farbtiefe, Farbtöne und Paletten gilt auch für Farbbilder. Wie kommt jedoch Farbe ins Spiel, was ist der Unterschied zwischen SW-Bildern und Farb-Bildern aus der Sicht von Farbtiefe und Farbtöne?

Auf der Seite Farbmodelle habe ich ausführlich verschiedene Farbmodelle, ihre Bedeutung, ihr Zustandekommen und wo sie eingesetzt werden beschrieben. Wichtig zu wissen ist, dass ein Bildschirm, ein Filmscanner oder eine Digitalkamera nach dem additiven Farbmodell arbeiten während ein Drucker nach dem subtraktiven Farbmodell arbeitet. Gemäß dem additiven Farbmodell erzeugt ein Computer-Bildschirm die unterschiedlichen Farbtöne, indem diese aus den drei Grundfarben rot, grün und blau zusammengesetzt werden. Aus diesem Grunde spricht man auch vom RGB-Farbmodell. Ein Bildpunkt besteht also aus drei verschiedenen Farbkanälen. An Fernsehgeräten sind deutlich pro Bildpunkt drei Lämpchen in roter, grüner und blauer Farbe zu erkennen; am Computerbildschirm ist die Auflösung zu hoch um einzelne Lämpchen zu erkennen. Was beim Monitor die einzelnen Lämpchen sind sind bei einem Scanner einzelne CCD-Zeilen, also auch pro Farbkanal eine.

Bei einem Farbbild entsteht ein Bildpunkt durch Überlagerung der drei Farbkanäle rot, grün und blau.

Farbe entsteht also durch Überlagerung der drei Farbkanäle rot, grün und blau. Für jeden einzelnen Farbkanal gilt genau dasselbe wie für den einen Farbkanal bei Schwarz/Weiß-Bildern: Die Anzahl der Bits gibt die unterschiedlichen Tonwertabstufungen pro Farbkanal an. Die kleinste denkbare Einheit ist wie beim SW-Bild 1 Bit Farbtiefe pro Farbkanal, also 3 Bit insgesamt. Für die einzelnen Farbkanäle bedeutet dies jeweils zwei Zustände: entweder schwarz oder rot/grün/blau (siehe erstes Bild in diesem Kapitel). Außer dem schwarzen Nichts und den drei Grundfarben können durch Mischung die vier zusätzlichen Farbtöne cyan, magenta, gelb und weiß entstehen.

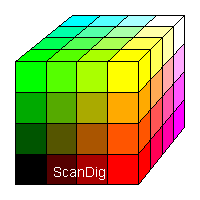
Das Mischen der Farben kann anschaulich anhand eines Farbwürfels gezeigt werden: Bei dem hier gezeigten Würfel hat das Bild eine Farbtiefe von 6 Bit, also 2 Bit pro Farbkanal. Damit können pro Farbkanal gemäß unserer Formel 2² = 4 Farbabstufungen dargestellt werden. Bei unserem Farbwürfel befindet sich in der linken unteren Ecke ein schwarzer Teilwürfel, in welchem alle drei Grundfarben den Wert Null haben. Rechts unten befindet sich der rote Teilwürfel und links oben der grüne Teilwürfel. Genau wie es bei einem Schwarz/Weiß-Bild eine lineare Grauskala von schwarz nach weiß gibt so gibt es bei Farbbildern eine lineare Skala von schwarz nach rot, von schwarz nach grün und von schwarz nach blau (unsichtbarer Teilwürfel hinten links unten). Dazwischen gibt es Farbtöne, die sich aus der Mischung der einzelnen Grundfarben ergeben; In der rechten oberen hinteren Ecke haben alle drei Grundfarben höchste Intensität, der entsprechende Teilwürfel ist also weiß; Nebenbei sei bemerkt, dass wir auf der Linie vom schwarzen Würfel links vorne unten zum weißen Würfel rechts oben hinten unsere Grauskala wieder finden. Grautöne entstehen also beim RGB-Farbmodell, indem sämtliche drei Grundfarben rot, grün und blau den gleichen Tonwert haben.

Bei einem Farbbild teilt sich die Gesamt-Farbtiefe auf die 3 Grundfarben auf. Für jede Grundfarbe gibt es eine eigene Tonwertskala von schwarz bis rot/grün/blau. Je nach Farbtiefe gibt es eine unterschiedliche Anzahl von Rottönen, Grüntönen und Blautönen auf jeder einzelnen Skala.

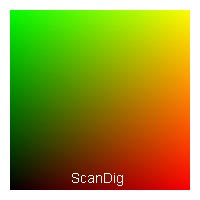
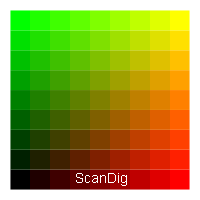
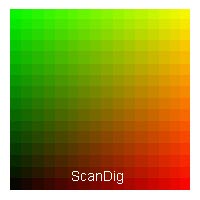
Das dritte Bild zeigt die vordere Seite des Farbwürfels bei einer Gesamt-Farbtiefe von 9 Bit. Das Gesamtbild besteht also aus 2⁹ = 512 Farbtönen. Pro Farbkanal stehen 3 Bit zur Verfügung, so dass es pro Farbkanal 2³ = 8 Abstufungen zwischen schwarz und rot/ grün/blau gibt. Im vierten Bild ist die Farbtiefe bereits 12 Bit, so dass sich insgesamt 2¹² = 4096 Farben ergeben. Pro Farbkanal sind also 4 Bit vorhanden, so dass sich jeweils 2⁴ = 16 einzelne Tonwerte pro Farbkanal ergeben. Man erkennt wie die Teilwürfelchen von Bild zu Bild immer kleiner werden und die Übergänge immer fließender werden.

Ein Farbbild wird normalerweise mit einer Farbtiefe von 24 Bit gescannt und gespeichert. Auch die meisten Computer-Bildschirme arbeiten mit einer Farbtiefe von 24 Bit. Eine Farbtiefe von 24 Bit bedeutet, dass insgesamt 2²⁴ ≈ 16.7 Millionen unterschiedliche Farbtöne dargestellt werden können. Bei einer solchen Vielzahl von Farben sagt man auch, dass ein Bild True Colors, also echte Farben hat. Eine Gesamt-Farbtiefe von 24 Bit bedeutet, dass pro Farbkanal 8 Bit zur Verfügung stehen. Vom tiefen schwarz bis zum kräftigen rot/grün/blau sind es also jeweils 2⁸ = 256 Tonwertabstufungen (vergleiche 8 Bit bei SW-Bildern). Unser fünftes Bild zeigt die Vorderseite des Farbwürfels wobei auf der horizontalen wie auch auf der vertikalen Achse jeweils 256 verschiedene Farbtöne gezeigt werden. Die Übergänge von schwarz nach rot bzw. grün sowie die Übergänge bis zum gelben Farbton erscheinen absolut fließend zu sein, wenngleich bei extremer Vergrößerung die einzelnen Schritte erkennbar wären.

Ein Farbbild wird üblicherweise mit 24 Bit Farbtiefe gespeichert und am Bildschirm dargestellt. Eine Farbtiefe von 24 Bit entspricht ca. 16.7 Millionen Farben und wird auch als True Colors bezeichnet.

Genauso wie bei Schwarz/Weiß-Bildern eine Farbtiefe von 8 Bit für die Darstellung am Bildschirm oder für Ausdrucke völlig genügt, reicht bei Farbbildern eine Farbtiefe von 8 Bit pro Farbkanal, also 24 Bit insgesamt, völlig aus um Bilder mit echten Farben am Bildschirm darzustellen oder auszudrucken. Wozu höhere Farbtiefen gut sind, darauf gehe ich später ein.

Verwendung von Paletten bei Farbbildern

Bei Schwarz/Weiß-Bildern haben wir gesehen, dass ein Bild mit 2 Bit Farbtiefe 4 ganz andere Grautöne haben kann als sie in einer linearen Grauskala von schwarz nach weiß vorkommen. Als Erklärung haben wir gelernt, dass die Farbtiefe von 2 Bit lediglich aussagt, dass das Bild aus maximal 2² = 4 verschiedenen Grautönen besteht, nicht jedoch welchen exakten Tonwert die einzelnen Grautöne haben. Vielmehr werden die exakten Tonwerte der einzelnen Grautöne aus dem Gesamtspektrum ausgesucht und in einer Palette gespeichert.

Gleiches gilt natürlich auch für Farbbilder; Ein Farbbild mit einer 2 Bit Palette kann wie ein SW-Bild 2² = 4 verschiedene Farbtöne enthalten. Die einzelnen Farbtöne können jedoch eine beliebige Kombination aus rot, grün und blau enthalten. Wie die Zuordnung der Palettenfarben zu den tatsächlichen Farben funktioniert, das überlassen wir unserem Betriebssystem, darum braucht man sich als Anwender nicht zu kümmern.

Betrachten wir das erste Bild in diesem Kapitel, so finden wir unser Matterhorn-Bild mit exakt 4 verschiedenen Farben dargestellt. Wir erkennen sofort, dass für den Himmel praktisch die Originalfarbe verwendet wurde während für die anderen Bereiche gut ausgesuchte Mischfarben zum Einsatz kommen. Vergleicht man dieses Bild mit dem entsprechenden Graustufenbild, so erkennt man ähnliche Strukturen auf dem Bild wieder. Die Farben wurden eben auf ähnliche Weise separiert und gruppiert.

Beim zweiten Bild erkennen wir das Matterhorn mit einer Farbpalette von 16 Farben wieder. Es ist derselbe Effekt wie beim entsprechenden Graubild zu erkennen: Die Strukturen werden fein aufgelöst, die Auflösung erscheint dadurch höher. Beim Himmel sind die gleichen Abstufungen zu erkennen wie beim Schwarz/Weiß-Bild. Hier wird genauso deutlich, dass man mit 16 Farben bereits gute Bilder auf dem Bildschirm darstellen kann, dass jedoch noch ein entscheidender Schritt fehlt bis ein wirklich gutes Bild zu sehen ist, denn die Abstufungen der 4 Blautöne am Himmel sind schon sehr störend.

Beim dritten Bild habe ich eine Palette mit 256 Farben verwendet; es handelt sich also um ein typisches GIF-Bild. Gegenüber dem Original (siehe ganz oben) sind kaum noch Unterschiede zu erkennen. Dies liegt aber im Wesentlichen an der verkleinerten fürs Internet optimierten Darstellung. Dies zeigt, dass für die Darstellung eines Bildes am Rechner eine Palette mit bescheidenen 256 Farben oftmals völlig ausreicht, dass man also nicht immer True-Color-Bilder benötigt.

Bei Farbbildern kann mit einer 256-Farben-Palette ein sehr ansehnliches Bild für die Darstellung am Rechner kreiert werden.

Auf die Darstellung der zugehörigen Tonwertkurven habe ich in diesem Kapitel verzichtet. Die Tonwertkurven sehen für jedes einzelne Bild wie die Tonwertkurven der entsprechenden Schwarz/Weiß-Bilder aus. Sie bestehen ebenfalls aus 4, 16 bzw. 256 einzelnen Balken, natürlich in unterschiedlicher Position für die einzelnen Farbkanäle.

Farbtiefe und Datentiefe

Bislang haben wir viel über das Thema Farbtiefe gesprochen, haben uns jedoch nie darum gekümmert, wie die entsprechenden Dateien überhaupt gespeichert werden. Auch geht aus den obigen Kapiteln klar hervor, dass ein Bild umso mehr Farben hat je größer die Farbtiefe ist. Dass dies nicht immer wahr ist zeigt folgendes Beispiel:

Ein ganz normales Bild, das im RGB-Modus abgespeichert wird, hat wie oben gelesen eine Farbtiefe von 24 Bit. Lädt man dieses Bild zum Beispiel in Photoshop^® und speichert es als CMYK-Bild, so steigt seine Dateigröße um ein Drittel an. Ein CMYK-Bild hat bekanntlich eine Farbtiefe von 32 Bit (jeweils 8 Bit für die einzelnen Kanäle cyan, magenta, yellow, black). Die Anzahl der möglichen Farbkombinationen ist mit 2³² ≈ 4 Milliarden um das 256-fache größer als bei normalen RGB-Bildern. Aber denkste!

CMYK-Bilder benötigt man für Drucke, wo jedem Farbkanal im Bild eine eigene Druckfarbe zugeordnet ist. Mit den drei Grundfarben Cyan, Magenta und Gelb kann man in der Theorie jeden Farbton zusammenmixen. In der Praxis ergibt Cyan + Magenta + Gelb jedoch kein reines schwarz sondern ein dunkles braun. Deshalb wird als vierte Farbe die sogenannte Key-Farbe Schwarz verwendet. Für die Anzahl der Farben bedeutet dies, dass unter den ca. 4 Milliarden theoretisch möglichen Farbkombinationen viele doppelt vorhanden sind. Entscheidend ist, dass der CMYK-Farbraum weniger Farben beinhaltet als der RGB-Farbraum. Unser Bild besteht also aus weniger Farbtönen wenn es im CMYK-Format anstatt im RGB-Modus abgespeichert ist! An diesem Beispiel wird deutlich, dass die 32 Bit große Datentiefe nichts mehr mit der tatsaechlichen Anzahl von Farbtönen zu tun hat.

Ein Bild hat im CMYK-Modus eine Datentiefe von 32 Bit, während es im RGB-Modus nur 24 Bit hat. Dennoch ist die Farbanzahl im RGB-Modus größer, da der RGB-Farbraum größer als der CMYK-Farbraum ist.

Als nächstes stellt sich die Frage wie groß eine Datei mit einem Bild einer bestimmten Farbtiefe ist. Ein normales Schwarz/Weiß-Bild hat wie oben gezeigt eine Farbtiefe von 8 Bit, ein Farbbild hat im RGB-Modus 3 mal 8 Bit, also 24 Bit. Pro Bildpunkt müssen also bei Schwarz/Weiß-Bildern genau 1 Byte und bei Farbbildern 3 Bytes auf der Festplatte gespeichert werden. Die Dateigröße in Bytes ergibt sich somit bei SW-Bildern ganz einfach aus der Anzahl der Bildpixel; bei Farbbildern ist die Dateigröße drei Mal so groß wie die Anzahl der Pixel. Beispiel: Ein 5-Megapixel Bild einer Digitalkamera benötigt als SW-Bild ziemlich genau 5 Megabyte und als Farbbild ungefähr 15 MByte auf der Festplatte.

Faustregel für die Dateigröße eines SW-Bildes bzw. Farbbildes auf der Festplatte oder im Speicher: Anzahl Bytes = Anzahl der Bildpunkte multipliziert mit 1 (Schwarz-Weiß) bzw. 3 (Farbe).

Diese Größenangabe bezieht sich natürlich auf ein unkomprimiertes Dateiformat wie TIF oder BMP. Bei komprimierten Bildformaten wie JPG oder GIF erhält man Dateigrößen, die sich nicht mehr direkt aus der Anzahl der Bildpunkte berechnen lassen.

Wozu benötigt man eine Farbtiefe von 48 Bit?

Die obigen Kapitel haben es gezeigt und ich habe es mehrfach betont, dass eine höhere Farbtiefe als 8 Bit bei Schwarz/Weiß-Bildern und 24 Bit bei Farbbildern zur Darstellung eines Bildes am Bildschirm oder auch für Ausdrucke keinen Sinn macht. Dennoch bieten viele Scanner größere Farbtiefen bis hin zu 48 Bit (also 16 Bit bei SW) an. Sind solche Angaben nur Augenwischerei und Geprotze oder gibt es handfeste Gründe für Scans mit bis zu 48 Bit Farbtiefe?

Zuerst unsere üblichen Berechnungen: Ein Schwarz/Weiß-Bild mit einer Farbtiefe von 16 Bit hat bis zu 2¹⁶ = 65.536 verschiedene Grautöne; bei 8 Bit Farbtiefe waren es nur 256. Ein Farbbild mit 48 Bit Farbtiefe hat pro Farbkanal 16 Bit, also jeweils 65.536 Farbton-Abstufungen. Insgesamt kommt man auf die unvorstellbare Anzahl von 2⁴⁸ = 281 Billionen Farbtönen. Was für ein Sprung gegenüber "nur" 16,7 Millionen bei einem normalen 24 Bit Bild!

Die astronomischen Zahlen, die bei der Verdoppelung der Farbtiefe entstehen, scheinen auf den ersten Blick wirklich nur Hochstapelei ohne praktische Bedeutung zu sein. Die folgende Anwendung zeigt jedoch, dass es durchaus Sinn macht, Scans mit einer höheren Farbtiefe zu machen. Die folgenden beiden Bilder zeigen eine langzeitbelichtete Astro-Aufnahme, die mit "nur" 24 Bit Farbtiefe gescannt wurde. Links ist das unbearbeitete gescannte Bild zu sehen, rechts das bearbeitete Bild mit Hervorhebung des Kernmotives.

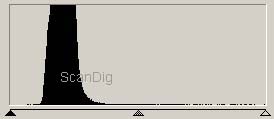
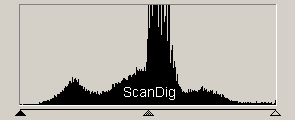
Betrachten wir die Tonwertkurve des linken unbearbeiteten Scans, so erkennen wir, dass 99% aller Tonwerte in einem schmalen dunklen Bereich liegen. Die Tonwertkurve zeigt übrigens eine statistische Verteilung aller Tonwerte eines Bildes auf einer Skala von schwarz (ganz links) bis weiß (ganz rechts), vergleiche die lineare Farbtonskala bei SW-Bildern von schwarz bis weiß. Derartige Tonwertkurven erhält man jedoch auch in Alltagssituationen, zum Beispiel bei Landschaftsaufnahmen mit bewölktem Himmel, wo das ganze Bild eine graue Einöde ist, oder bei Strandaufnahmen, wo Wasser und Himmel praktisch ein einziges Blau bilden.

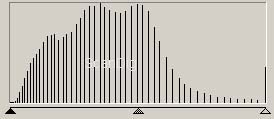
Um dem Bild mehr Kontrast zu verleihen und damit das Kernmotiv gegenüber dem Hintergrund hervorzuheben, schneidet man die Tonwertkurve links und rechts des dicken schwarzen Bereiches ab. Als Resultat erhält man das rechte bearbeitete Bild in dem der fotografierte Nebel prächtig zu sehen ist. Betrachten wir jedoch die darunter liegende Tonwertkurve, dann stellen wir fest, dass etwas Schreckliches passiert ist: Von den im linken Bild vorhanden 256 Tonwerten pro Farbkanal wurden Ca. 50 freigeschnitten. Diese ca. 50 verbleibenden Tonwerte pro Farbkanal sind in der rechten Tonwertkurve verstreut zwischen schwarz (ganz links) und weiß (ganz Rechts) wiederzufinden. Die großen Lücken in der Tonwertkurve bedeuten, dass entsprechende Farbtöne gar nicht mehr besetzt sind.

Durch die Tonwertkorrektur im Bildbearbeitungsprogramm haben wir also ein Bild erhalten, welches zwar ganz normal als 24 Bit Datei gespeichert wird, jedoch haben wir effektiv ca. 80% aller Tonwerte pro Farbkanal verloren, so dass ein sehr farbarmes Bild übrig bleibt. Dieses Bild mag am Bildschirm vielleicht noch ansehnlich sein, beim großformatigen Ausdruck erkennt man jedoch krasse Übergänge wie im Kapitel SW-Bilder mit 4 Bit Farbtiefe gezeigt.

Hätte ich das linke Bild dagegen mit 48 Bit Farbtiefe gescannt so würde die linke Tonwertkurve 65.000 Farbabstufungen pro Kanal darstellen; das Aussehen der Tonwert-Kurve wäre dabei identisch. Nach dem Abschneiden von 80% aller Farbtöne pro Kanal blieben immer noch über 12.000 Farbtöne pro Kanal, also genug um beim Abspeichern des Bildes in Form einer normalen 24 Bit-Datei die notwendigen 256 Abstufungen pro Kanal zu erhalten. Die rechte Tonwertkurve hätte einen identischen Verlauf, jedoch wären keine Lücken zwischen den einzelnen Balken mehr vorhanden.

Fazit: Scans mit höheren Farbtiefen als 24 Bit machen sehr wohl Sinn, wenn man nach dem Scannen eine aufwändige Bildbearbeitung durchführt.

Abschließend möchte ich noch bemerken, dass zu einem 48 Bit Scan auch ein entsprechendes Bildbearbeitungsprogramm gehört. Viele Bildbearbeitungs-Programme, darunter auch Adobe^® Photoshop^® Elements, sind gar nicht in der Lage mit 48-Bit Dateien umzugehen. Die Größe einer Bilddatei verdoppelt sich übrigens beim Übergang von 24 Bit auf 48 Bit bei Farbbildern bzw. von 8 Bit auf 16 Bit bei Schwarz/Weiß-Bildern.

Tipps für die Scan-Praxis

Wer alle oben stehenden Kapitel sorgfältig gelesen hat weiß jetzt mit Sicherheit mit dem Begriff Farbtiefe umzugehen und entsprechende Zahlenangaben zu interpretieren. Was jetzt vielleicht noch fehlt sind ein paar handfeste Tipps für die Praxis beim Scannen seiner Fotos oder für die Kaufentscheidung eines Filmscanners. Bitte schön...

Auf den Datenblättern moderner Filmscanner findet man zumeist Farbtiefen von 24, 36, 42 oder gar 48 Bit. Diese Angaben bedeuten noch lange nicht, dass der Scanner wirklich so viele einzelne Farbtöne liefert. Diese Angaben auf einem Filmscanner-Datenblatt bedeutet lediglich, dass der A/D-Wandler im Scanner-Inneren die analogen Signale des CCD-Sensors mit entsprechend vielen Abstufungen an die Scan-Software weitergeben kann. Wie viele Farben der Scanner tatsächlich detektieren kann hängt von vielen anderen Faktoren wie den verwendeten Linsen oder der Elektronik ab.

Die Angabe der Farbtiefe auf dem Datenblatt eines Filmscanners gibt nur die Anzahl möglicher Signale beim A/D-Wandler an, hat mit der tatsächlichen Anzahl der Farbtöne also nicht viel zu tun.

Wer seine Bilder einfach nur einscannt, um sie anschließend am Bildschirm zu betrachten oder sie auszudrucken kann sich bei Farbbildern mit der Standard-Farbtiefe von 24 Bit und bei Schwarz/Weiß-Bildern mit 8 Bit begnügen. Wer jedoch das Maximum an Information aus seinem Filmmaterial herausholen möchte und jedes Bild einer anschließenden eingehenden Bildbearbeitung unterziehen möchte sollte seine Scans mit der höchst möglichen Farbtiefe durchführen.

Es gibt nur wenige Bildformate, die überhaupt 48 Bit-Bilder aufnehmen koennen. Die bewährten Formate JPG oder GIF sind reine 24 Bit Formate, können also Bilder mit mehr Farbinformation gar nicht abspeichern. Ein gängiges Grafikformat zur Aufnahme von 48 Bit Bildern ist das TIF-Format. Da 48 Bit Bilder jedoch sehr groß sind sollte man ein verlustfreies Kompressionsverfahren wie LZW anwenden.

Wer wirklich hohe Ansprüche hat und 48 Bit Scans macht sollte die Originalscans unbearbeitet im TIF-Format auf DVD sichern. Die bearbeiteten Bilder speichert man dann besser in einem stark komprimierten TIF- oder JPG-Format separat ab.

Zurück zum Inhaltsverzeichnis Farbmanagement