El factor de luminancia (factor de ganancia)
Las personas que piensan comprar una pantalla de proyección para el uso doméstico o profesional tropezarán repetidamente con el factor de luminancia mencionado en la hoja de datos, también llamado factor de ganancia. En el caso de muchas pantallas, este parámetro importante es indicado como una especie de dato de rendimiento como la frecuencia de tacto del procesador de un ordenador o el tamaño de un disco duro en gigabytes.
Pero detrás del término factor de ganacia se encuentra mucho más que un dato de rendimiento; caracteriza el comportamiento de radiación de la luz de una pantalla a una dirección determinada. Por eso, en realidad no tiene mucho sentido indicar el factor de ganancia de una pantalla con un mero número. Lo que hay exactamente detrás de ello y lo que se puede deducir de un mero número en la hoja de datos de una pantalla se especificará detalladamente en el capítulo siguiente.
Introducción y motivación
Antes de dedicarnos a la definición física-matemática del factor de luminancia vamos a intentar a comprender la problemática a base de unos fenómenos de la vida diaria. Las personas que todavía se pueden recordar de los tiempos del comienzo de las pantallas planas saben que con los primeros modelos, el usuario que se encontraba directamente delante de la pantalla podía disfrutar de una imagen espléndida y sin interferencias. Pero en cuanto esta persona quería enseñar algo de la pantalla a sus amigos o colegas y se juntaba un pequeño grupo de personas a su alrededor, se generaba un gran vayven y movimientos hacia arriba y abajo, porque la imagen sólo se podía ver óptimamente desde el punto de vista frontal. Hoy en día, esta problemática casi está completamente resuelta, aunque en el caso de algunas pantallas TFT de bajo coste tampoco se puede reconocer una imagen perfecta vista del lado extremo.
Vamos a imaginar este fenómeno en una sala de cine: los espectadores en los asientos centrales disfrutan de una imagen perfecta, mientras las personas sentadas en los bordes perciben una imagen muy débil. Esto no es aceptable! Por lo tanto, en un cine, la pantalla debe ser estructurada de tal manera que radie la luz entrante de manera uniforme y en una buena margen de ángulo, de forma que el espectador pueda disfrutar plenamente de la película.
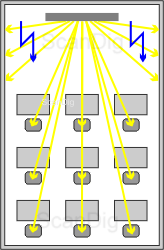
Pero también existe una situación contrárea: en los tiempos del principio cuando los proyectores y los vídeoproyectores aún tenían una luz muy débil se intentaba evitar el desperdicio de la luz. En una habitación estrecha dónde los espectadores están sentados en unas filas, no tiene ningún sentido reflejar gran parte de la luz radiada a las paredes laterales; finalmente, la imagen debe alcanzar a los espectadores y no a la pared. Para evitar el oscureciemiento completo de la habitación durante el uso de un proyector de luz débil, la pantalla de proyección debería concentrar la luz hacia la dirección de los espactadores y no radiarla a todas las direcciones.
La imagen contígua representa esta problemática: en una sala de enseñanza alargada, dónde 9 participantes contemplan la pantalla del lector como hechizados , el ángulo de visión de los espectadores oscila entre 0° y 30°. La luz que es radiada en un ángulo más grande por la pantalla directamente a las paredes es desperdiciada y tampoco deseada, es decir que gran parte de la luz radiada por el proyector no llega a los espectadores. Si el vídeoproyector en uso es de luminancia muy intensa, esta pérdida por divergencia no tiene importancia e incluso se puede proyectar durante el día. Pero al contrario, en el caso de un vídeoproyector débil se desperdicia más de la mitad de la luz proyectándola a la pared de forma que llega uy poca luz a los espectadores y se tiene que oscurecer la habitación artificialmente. Como el proyector o el videoproyector no puede determinar como la luz que radia es reflejada, la tarea de la pantalla es concentrar y reflejar la luz incidente de tal forma que llegue al público de forma uniforme y no a la pared.
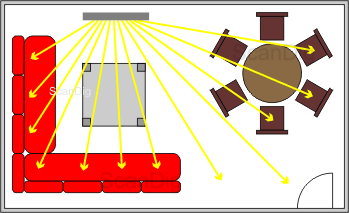
Ahora veremos un típico salón alemán con un rincón de sofás y un rincón para comer. Aquí las condiciones son muy distntas que en nuestra sala de enseñanza: hay un sitio para el "jefe" en el sillón, que es quién mira directamente de frente a la pantalla. Pero también el resto de la familia que se acomoda en el sofá quiere disfrutar plenamente de la película. Incluso también puede haber una parte de la familia sentada en la mesa para comer que sólo quiere enterarse "de paso" de las escenas de suspense de la película. Por lo tanto, en un salón semejante, el público se encuentra en una zona angular que oscila entre aproximadamente 0° - 80° hacia los dos lados. Todos quieren obtener algo de la luz que dispersa la pantalla. Al contrario de nuestra sala de enseñanza, la luz debe ser repartida uniformemente hacia todas las direcciones; eventualmente, el sillón del jefe en frente de la pantalla se usará con más frecuencia, de forma que la radiaciación debe ser especialmente buena en este sitio. Una situación parecida hay en el cine dónde el ángulo de visión de los mejores asientos es de 0° horizontal y verticalmente hasta unos altos grados de ángulo para los sitios al borde de la primera fila.
Por lo tanto, vamos a concluír este capítulo diciendo que hay situaciones distintas en las que la pantalla en uso debe de efectuar un efecto determinado relacionado con la luz incidente y esta es la razón por la que hay distintos tipos de pantalla. Y para no tener que definir este efecto sólo con palabras generales sino también con un valor numérico, vamos a introducir a continuación el tal llamado factor de luminancia.
Definición del factor de luminancia
En el capítulo anterior hemos determinado a base de algunos ejemplos prácticos que deben existir distintas pantallas con distintos tipos de características de reflejo para cada situación de proyección. Expresado de una manera más técnica, esto quiere decir
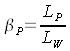 que una pantalla determinada debe de reflejar la luz incidente con una cierta intensidad a una dirección y con otra intensidad a otra dirección. Para poder describir la intensidad de reflexión con un valor numérico utilizamos el factor de luminancia β. Ahora, vamos a atrevernos a saltar al agua fría y vamos a leer una vez la definición del factor de luminancia como está especificado en la norma alemana DIN 19045-4 ("Proyección de imágenes fijas e imágenes animadas, 4° parte: características de reflexión y de transmisión de las pantallas de proyección"):
que una pantalla determinada debe de reflejar la luz incidente con una cierta intensidad a una dirección y con otra intensidad a otra dirección. Para poder describir la intensidad de reflexión con un valor numérico utilizamos el factor de luminancia β. Ahora, vamos a atrevernos a saltar al agua fría y vamos a leer una vez la definición del factor de luminancia como está especificado en la norma alemana DIN 19045-4 ("Proyección de imágenes fijas e imágenes animadas, 4° parte: características de reflexión y de transmisión de las pantallas de proyección"):
Definición: el factor de luminancia βP es, según DIN 5036, la relación de la luminancia LP de una muestra de pantalla para una dirección de visión determinada a la luminancia LW de la superficie perfectamente dispersante y reflejante (estándar blanco) para la dirección incidental determinada.
Todo entendido? O no ha entendido nada? Naturalmente, una definición semejante es un pequeño desafío, ya que también indica otra norma, la DIN 5036. Vamos a intentar aclarar la cuestión. Primero hemos tropezado dos veces con el término luminancia. En nuestra página de fotometría he descrito exactamente lo que se entiende bajo el término luminancia: se trata de una medida para la luminosidad de una fuente de luz y/o de una superficie que refleja la luz. Más fuerte que radia la superficie, más grande es su luminancia; además, la luminancia es más grande cuando la superficie radiante es más pequeña. Si simplemente memorizamos que la luminancia indica la luminosidad con la que una pantalla determinada radia a una dirección determinana, podemos entender la definición del factor de ganancia:
Vamos a coger un pequeño trozo de nuestra pantalla de proyección, una tal llamada muestra de pantalla, y la radiamos. Entonces medimos la luminancia con la ayuda de un tal llamado fotómetro hacia una dirección determinada, por ejemplo verticalmente a esta superficie. Por lo tanto, nuestro fotómetro nos aporta un cierto valor numérico para la luminancia LP de nuestra pantalla. Entonces cambiamos nuestro trocito de pantalla por otro trozo de pantalla, siendo esta perfectamente reflejante hacia todas las direcciones y medimos otra vez con nuestro fotómetro la luminancia LW. Ahora tenemos dos valores de medida de los cuales podemos calcular el cociente y así obtener el factor de luminancia. Queda la pregunta de qué es una superficie perfectamente dispersante y reflejante.
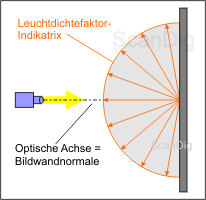
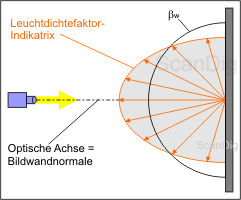
Para ello, vamos a contemplar la imagen de arriba, en la cual una pantalla es radiada verticalmente por una fuente de luz; esto quiere decir que el eje óptico de la luz equivale al de la perpendicular de la pantalla. Por lo tanto, el rayo de luz cae verticalmente sobre la pantalla y es reflejado por ella. El término "perfectamente reflejante" de la definición de arriba significa que toda la luz incidente es reflejada, por lo tanto ni la más mínima cantidad es absorbida o transmitida.
Pero el término "perfectamente dispersante" es más importante en esta definición: esto quiere decir que la luz incidente es perfectamente dispersada a todas las direcciones. Esto se representa en la imagen mediante un semicírculo que, en la realidad es naturalmente una hemiciclo. Por lo tanto, la luz incidente es dispersada sin ninguna pérdida y uniformemente hacia todas las direcciones, de forma que se obtiene la misma cantidad de luz de cada ángulo hacia la pantalla. Una superficie con estas características se llama estándar blanco que en la práctica sólo se obtiene aproximadamente. El semicírculo que visualiza la intensidad de la reflexión de la luz hacia distintas direcciones se llama técnicamente Indicatrix del factor de luminancia. Ahora podemos resumir que una pantalla con semejantes características uniformes tiene un factor de ganancia de 1,0 para todas las direcciones.
El indicatrix del factor de luminancia visualiza el comportamiento de radiación de una pantalla. Para una superficie perfectamente dispersante y reflejante (estándar blanco) es un semicírculo que simboliza el factor de luminancia de 1 hacia todas las direcciones.
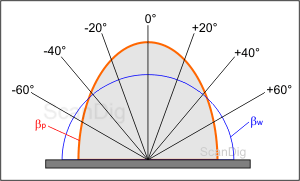
Ahora, la pregunta es cómo es una indicatrix semejante para una pantalla auténtica? En la imagen siguiente demostramos un ejemplo para un tipo de pantalla D. El semicírculo negro demuestra la indicatrix para nuestra superficie perfectamente dispersante y reflejante de la imagen anterior como referencia. El factor de ganacia correspondiente es βW = 1. El semi-elipse rojo demuestra la indicatrix real del factor de la luminancia para esta pantalla. He de mencionar nuevamnete que en realidad no se trata de un elipse sino de un elipsoide; este se obtiene si se rota el elipse demostrado con el marco rojo por el eje óptico.
Comparando el elipse rojo con el semicírculo negro, leemos que esta pantalla refleja más intensamente a la dirección de la perpendicular de pantalla que hacia el borde. Por lo tanto, el factor de ganancia es, en dirección de la vertical, de aproximadamente 1,2. Al contrario, para el factor de ganancia verticalmente a la perpendicular leemos un valor de sólo 0,8. Y en un ángulo de aproximadamente 60° al eje óptico, el elipse rojo se intercorta con el semicírculo negro; aquí, el factor de ganancia es de exactamente 1,0. Por lo tanto, se puede describir el comportamiento de una pantalla semejante de aproximadamente esta manera: la persona que se encuentra directamente de frente obtendrá mucha luz; la persona que esté en una posición diagonal hacia la pantalla percibirá unas condiciones de luz normales; aquella persona que mire la pantalla desde un lado, aún reconocerá la imagen. El mejor sitio de la habitación para contemplar la pantalla depende, naturalmente, de la luminancia del proyector y de la luminosidad de la habitación.
Especialmente contemplando la segunda imagen todos deben entender lo que es el factor de luminancia. Y - esto es muy importante - también se aclara que el comportamiento de radiación de una pantalla no se puede describir con un mero factor, ya que el factor de ganancia sólo se aplica para una dirección determinada. Para describir el comportamiento de reflexión de una pantalla, el productor debería indicar el factor de ganancia para distintos ángulos de visión o simplemente adjuntar una foto del indicatrix del factor de luminancia. Este punto también es tan importante para mí que voy a destacarlo nuevamente:
El factor de ganancia indica el comportamiento de reflejo de una pantalla a una dirección determinada. Para describir el comportamiento de radiación de una pantalla se necesita o bien una tabla con los factores de ganancia en los ángulos determinados o una visualización gráfica en forma de un indicatrix del factor de luminancia.
Considerando este hecho, qué sentido tiene si el productor describe una pantalla determinada con un factor de ganancia de 1,2? Según lo dicho arriba, es cierto que este valor sólo es válido para una dirección determinada, la perpendicular, pero de este valor en dirección al perpendicular se puede derivar aproximadamente el comportamiento de reflexión hacia las otras direcciones, según la foto de arriba.
Medición del factor de ganancia
Ahora que sabemos qué es el factor de ganancia y los dos valores (luminancia) de los cuales es calculado, la pregunta es cómo se mide el factor de ganancia para una pantalla. Según la definición del factor de ganancia, esto suena muy fácil: compramos un aparato para la medición de la luminancia, radiamos un trozo de pantalla, medimos la luminancia, entonces reemplazamos este trozo de pantalla por una pantalla de norma, volvemos a medir y creamos el cociente.
Pero este asunto no es así de fácil. Primero necesitamos una fuente de luz apta, y aquí no es suficiente utilizar una lámpara cualquiera sino una que produce la norma de luz A según DIN 5033-7. Una fuente de luz semejante se puede adquirir, al igual que el aparato para medir la luminancia, en comercios especializados. Pero el verdadero problema es conseguir una superficie perfectamente dispersante y reflejante, porque algo así no existe en realidad. En cambio, se utilizará una tal llamada norma para la reflexión. Esto es - expresado de forma simple - un pequeño trozo de pantalla que no es ni perfectamente dispersante ni perfectamente reflejante pero cuyas
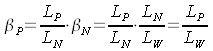 características son conocidas. Dicho de otra manera, una norma para la reflexión semejante ya contiene el indicatrix correspondiente en forma de un esquema o gráfico; por lo tanto, para cada ángulo de visión conocemos el factor de luminancia βN correspondiente que forma el cociente de la luminancia de la perpendicular de reflexión y la luminancia. Si efectuamos la medición de la luminancia una vez con una muestra de pantalla (nuestra pantalla verdadera) LP y una vez con la norma de reflexión LN, obtenemos, según la fórmula de arriba, nuestro factor de ganancia βP. Aquí, tambien se debe destacar que debemos medir y calcular el factor de luminancia individualmente para cada ángulo de visión; por lo tanto, siempre obtenemos un βP(ε), siendo ε el ángulo de visión relativo a la perpendicular de la pantalla. Vamos a resumir los mensajes principales de este capítulo en una casilla:
características son conocidas. Dicho de otra manera, una norma para la reflexión semejante ya contiene el indicatrix correspondiente en forma de un esquema o gráfico; por lo tanto, para cada ángulo de visión conocemos el factor de luminancia βN correspondiente que forma el cociente de la luminancia de la perpendicular de reflexión y la luminancia. Si efectuamos la medición de la luminancia una vez con una muestra de pantalla (nuestra pantalla verdadera) LP y una vez con la norma de reflexión LN, obtenemos, según la fórmula de arriba, nuestro factor de ganancia βP. Aquí, tambien se debe destacar que debemos medir y calcular el factor de luminancia individualmente para cada ángulo de visión; por lo tanto, siempre obtenemos un βP(ε), siendo ε el ángulo de visión relativo a la perpendicular de la pantalla. Vamos a resumir los mensajes principales de este capítulo en una casilla:
Para la medición del factor de luminancia βP(ε) se necesita una fuente de luz de norma, un aparato para la medición de la luminancia y una norma para la reflexión con un comportamiento de reflexión conocido βN(ε). Para cada dirección de contemplación ε la medición tiene que ser invididual.
Finalmente, he de mencionar que este procedimiento para la medición que aún lo he descrito de una forma relativamente sencilla en realidad es muy laborioso y complicado. Y, no por último, no hay ninguna norma para la reflexión aplicable que mantenga sus características técnicas de la luz permanentemente; y, adicionalmente, también las normas para la reflexión aplicables deben ser repetidamente calibradas con verdaderas normas para la reflexión.
Representación del factor de luminancia mediante las curvas dispersantes
En el capítulo anterior hemos aprendido que el factor de luminancia βP(ε) sólo se puede medir en una vez para un ángulo de visión determinado β. Por lo tanto, para poder hacer una declaración fundida sobre el comportamiento de radiación de una pantalla de proyección se necesitan varias medidas individuales con distintos ángulos de visión.
| Ángulo de visión |
Factor de luminancia |
| 0° |
1,4 |
| ± 20° |
1,2 |
| ± 40° |
1,05 |
| ± 60° |
0,8 |
Resumiendo una serie de medición semejante en una tabla en la cual se indica el factor de luminancia respectivo para distintos ángulos de visión, se puede crear fácilmente una visión general del comportamiento de la reflexión de una pantalla. Aquellos valores que no aparecen en la tabla se pueden calcular mediante la interpolación. Pero para obtener rápidamente la visión general sobre el comportamiento de radiación de la pantalla y sobre todo para poder comparar distintas pantallas, una tabla del factor de ganancia es menos apta. Para ello, la visión gráfica del comportamiento de la reflexión es más recomendable.
Existen dos formas de representación habituales para el factor de luminancia: el uso de las coordenadas cartesianas o el uso de coordenadas polares. Vamos a empezar con las curvas de distribución en forma de coordenadas polares que ya hemos conocido "de paso" en el penúltimo capítulo. La imagen adyacente visualiza literalmente el comportamiento de reflexión de una pantalla.Partiendo de la perpendicular de la pantalla (línea 0°, aquí 20°). Estas líneas representan una dirección de contemplación determinada. La curva de referencia de blancos azul sirve como curva de referencia con un factor de ganancia constante de 1. Notamos los datos medidos para el factor de luminancia en las líneas angulares respectivas y comunicamos estos puntos formando la curva roja que visualiza el comportamiento de reflexión de la pantalla para el ángulo incidental de luz de 0°.
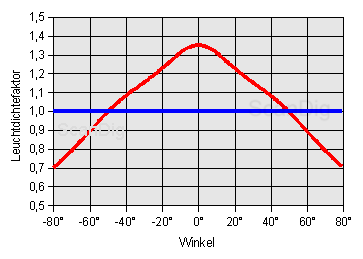
Un modo alternativo para la representación de la curva de distribución del factor de luminancia es mediante las coordenadas cartesianas. La imagen adyacente demuestra exactamente el mismo contenido que el de la imagen de arriba de las coordenadas polares. Aquí notamos como en una gráfica normal cada ángulo de visión en el eje x y en el eje y el factor de luminancia correspondiente. Nuestra curva de referencia de blancos azul con el factor de ganancia constante de 1 se convierte en la gráfica en una recta y nuestra curva de distribución para la pantalla medida se convierte en un montana simétrica. Las ventajas de esta forma de la representación es que podemos leer los valores numéricos directamente de la gráfica y que reconocemos claramente la caída de la luminancia en la zona del máximo.
La mejor forma de representar la curva de distribución depende de la forma de aplicación de ella. La persona que desea tener una gran visión general sobre el comportamiento de reflexión de una pantalla estará mejor servida con la gráfica de las coordenadas polares; pero aquellas personas que necesitan unos valores numéricos concretos para el dimensionamiento de una habitación profesional de presentaciones necesitarán la representación cartesiana.
Finalmente quiero enfatizar que tanto la forma tabular del ángulo de visión y el factor de ganancia respectivo como también la visualización en coordenadas polares o cartesianas tienen el mismo contenido físico.
Volver al índice pantallas de proyección
|