Facteur de luminance (facteur Gain)
Celui qui achète un écran pour le domaine privé ou professionnel rencontre tout le temps dans des fiches de produit/fiche technique et des prospectus, le facteur de luminance qui est aussi qualifié de facteur Gain ou de Gain simple. Ce paramètre important est spécifié dans de nombreux écrans comme un genre vanté de la caractéristique de performance comme la fréquence du processeur pour un ordinateur ou la taille d'un disque dur spécifié en gigaoctet.
Derrière le facteur Gain, il y a bien plus qu'une dimension de performance; il caractérise la réflexion de la lumière d'un écran dans une direction précise. Pour cette raison, il n'y a pas vraiment beaucoup de sens d'indiquer le facteur Gain comme un simple nombre pour un écran. Ce qui se trouve exactement derrière cela et ce qu'on peut faire avec un nombre nu dans la fiche produit/fiche technique d'un écran, les chapitres suivants doivent l'expliquer en détail.
Introduction et motivation
Avant d'essayer de trouver la définition physique et mathématique du facteur de luminance nous devons comprendre la problématique avec quelques phénomènes connus du quotidien. Celui qui peut encore se souvenir des premiers temps des écrans plats sait, qu'avec les premiers modèles l'utilisateur qui a été assis directement devant l'écran, a pu prendre plaisir avec une image scintillante splendide. Dès qu'il a voulu présenter cependant ce phénomène à quelques amis ou à des collègues et placé un petit groupe de gens autour de l'écran, il est apparu un grand tremblement de l'image qui n'a pu être reconnue parfaite qu'à la vue frontale. Cette problématique est résolue largement de nos jours, bien que pour quelques écrans à bas prix, le TFT avec une vue de côté extrêmement forte, montre qu'aucune image propre ne peut non plus être reconnue.
Nous imaginons ce phénomène dans un cinéma: Les invités du cinéma les plus heureux sur les sièges centraux jouissent d'une image parfaite tandis que les "personnages secondaires" perçoivent une image fortement atténuée. Inacceptable! L'écran du cinéma doit être conçu de telle manière, que la lumière incidente diffuse régulièrement dans un bonne zone angulaire de sorte que chaque spectateur réalise entièrement un bénéfice de ses frais.
Toutefois, il y a aussi la contre-situation: Dans les premiers temps, lorsque le beamer et les projecteurs étaient encore très lumière faibles, on ne voulait perdre aucune lumière. Dans une pièce étroite, où les spectateurs sont assis dans des rangs serrés l'un derrière l'autre, il ne fait pas de sens de réfléchir une grande partie de la lumière diffusée aux piédroits; l'image doit joindre finalement le spectateur et non pas le mur. Pour éviter un assombrissement total de la pièce lors de l'utilisation d'un projecteur de lumière faible, l'écran projecteur devrait focaliser la lumière d'une manière ou d'une autre en direction du public et ne pas la diffuser dans toutes les directions.
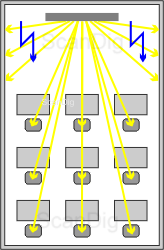
L'image à côté doit expliquer cette problématique: Dans une salle de formation allongée, où 9 participants de formation envoûtés regardent l'image de l'écran du professeur, l'angle de contemplation des spectateurs se trouve dans une zone angulaire entre 0° et 30°. La lumière que diffuse l'écran dans une plus grand zone angulaire sur les murs, est indésirable c.-à-d. une grande partie de la lumière diffusée par le projecteur, n'arrive pas du tout chez les spectateurs. Si le beamer utilisée a une grande intensité de luminance, cette perte de diffusion ne joue pas un rôle et il peut être même projetée lors de la journée. Si plus de la moitié de la lumière sera projetée en dehors de la fenêtre et sur le mur, le public recevra que trop peu de lumière et la pièce doit être assombrie artificiellement. Celui qui ne peut pas déterminer, comment sera réfléchie la lumière diffusée du Beamer ou du projecteur, il doit savoir que la tâche de l'écran de projection se concentre à la focalisation et le réflexion de la lumière pénétrante, de sorte à ce qu'elle arrive au public et pas aux murs extérieurs.
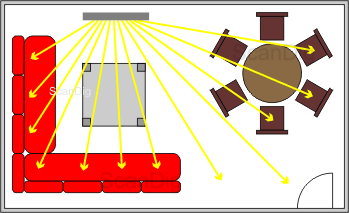
Si nous observons comme deuxième exemple une salle de séjour typiquement allemande avec un coin de canapé et un coin-repas. Ici, nous avons des conditions toutes à fait différentes que dans notre salle de formation: Il y a la position de chef sur le canapé, à savoir celui qui regarde directement sur l'écran. Mais aussi le reste de la famille qui s'assied confortablement sur le canapé, voudrait aussi pouvoir jouir du film. Une partie de la famille est éventuellement assise à la table et voudrait voir quelque chose des scènes passionnantes du film. Dans une telle salle de séjour, le public est alors assis dans une zone angulaire d'environ 0°- 80° répandu dans les deux directions. Tous veulent recevoir un peu de la lumière de l'écran. Contrairement à notre salle de formation, la lumière doit être réfléchie régulièrement dans toutes les directions; le fauteuil de chef est éventuellement dans l'usage fréquent que les autres places assises, de sorte qu'il peut être bien réverbéré en direction de cette place. Une situation semblable règne aussi dans un cinéma où l'angle de contemplation des meilleures places se situe au niveau de 0° horizontal et vertical jusqu'à des degrés angulaires élevés pour les places de bord dans le premier rang.
Nous soutenons alors fermement à la fin de ce sous-chapitre, qu'il y a des situations différentes, dans lequel l'écran correspondant doit obtenir un effet tout à fait précis, en ce qui concerne la réflexion de la lumière incidente. J'anticipe qu'il y a de nombreux types d'écrans différents à cause de cet effet. Et pour ne pas pouvoir seulement décrire cet effet avec des paroles générales mais aussi numériques, nous introduisons maintenant le facteur de luminance.
Définition du facteur de luminance
Dans le chapitre précédent, nous avons constaté avec quelques exemples concrets qu'il devait y avoir de différents écrans de projections avec des qualités de réflexion diverses pour satisfaire à chaque situation de projection. Exprimé professionnellement, ceci signifie,
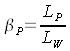 qu'un écran précis doit réfléchir la lumière incidente avec une intensité tout à fait précise dans l'une ou autre direction. Pour décrire numériquement l'intensité de la réflexion, nous utilisons le facteur de luminance β. Osons le saut dans l'eau froide et lisons une fois la définition du facteur Gain, comme elle se trouve dans la norme allemande DIN 19045-4 ("projection d'une image portrait ou de course, partie 4: Qualités de réflexion et de transmission des images au murs "):
qu'un écran précis doit réfléchir la lumière incidente avec une intensité tout à fait précise dans l'une ou autre direction. Pour décrire numériquement l'intensité de la réflexion, nous utilisons le facteur de luminance β. Osons le saut dans l'eau froide et lisons une fois la définition du facteur Gain, comme elle se trouve dans la norme allemande DIN 19045-4 ("projection d'une image portrait ou de course, partie 4: Qualités de réflexion et de transmission des images au murs "):
Définition: Le facteur de luminance βP est selon DIN 5036 le rapport de la luminance lumineuse LP d'un essai d'image murale pour une direction de contemplation donnée sur la luminance lumineuse LW de la surface complètement réfléchie (blanc standard) pour une direction d'irradiation fixée à l'avance.
Tout va bien? Ou rien compris? Une telle définition est bien sûr une chose spéciale, parce qu'elle renvoie sur d'autres normes DIN 5036. Nous essayons d'apporter un peu de lumière dans l'obscurité. D'abord, nous trébuchons deux fois sur l'idée de la luminance lumineuse. Sur notre page de photométrie j'ai déjà décrit ce que l'on entend par la luminance lumineuse: Il s'agit d'une mesure pour la luminosité d'une source lumineuse ou d'une lumière d'une surface réfléchit. Plus fortement la surface rayonne, plus grande sera sa luminance lumineuse; en outre, la luminance lumineuse est plus grande d'autant plus petite est la surface rayonnante. Si nous nous remarquons simplement que la luminance lumineuse indique à quel point une surface rayonne clairement dans une direction précise, afin de comprendre la définition du facteur Gain:
Nous prenons un petit morceau de notre mur de projection, un prétendu essai d'image murale, et on rayonne celle-ci. Ensuite, nous mesurons à l'aide d'une prétendue photomètre la luminance lumineuse dans une direction tout à fait précise, par exemple verticalement à cette surface. Notre photomètre nous donne alors une certaine valeur numérique pour la luminance lumineuse LP de notre essai d'image murale. Nous échangeons notre petit morceau d'écran contre un autre morceau de surface d'affichage, de sorte que cette surface doit être parfaitement réfléchissante dans toutes les directions et nous mesurons de nouveau avec notre photomètre la luminance lumineuse LW. Maintenant nous avons deux valeurs de quoi nous pouvons calculer le quotient pour avoir le facteur de luminance. Il reste encore la question qu'est ce qu'une surface parfaitement diffuse et réfléchissante.
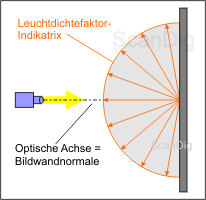
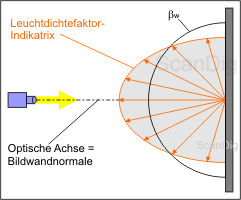
Pour cela, nous observons l'image ci-dessus sur laquelle une image murale lumineuse sera rayonnée verticalement d'une source lumineuse; cela signifie que l'axe optique de la lumière est tout de suite les normaux de l'image murale. Le rayon lumineux heurte alors verticalement l'écran et sera réfléchie par celle-ci. Le terme "parfaitement réfléchi" dans la définition ci-dessus signifie que toute la lumière incidente sera réfléchie mais aucune petite quantité n'est absorbée (avalée) ou transmise (laisser passe).
Le plus important dans la définition est cependant la notion "parfaitement diffuse": Cela signifie que la lumière incidente sera parfaitement diffuse dans toutes les directions. Dans l'image, ceci est représenté par un demi-cercle qui est bien sûr un hémisphère dans la réalité. La lumière incidente est alors diffusée régulièrement sans concession dans toutes les directions, de sorte qu'on obtient la même quantité de lumière de chaque angle de l'image murale lumineuse mur de projection. On qualifie une surface avec de telles qualités comme un blanc standard que l'on trouve qu'approximativement dans la pratique. On qualifie dans le langage technique le demi-cercle qui illustre l'intensité de réflexions de la lumière dans différentes directions avec l'indicatrice du facteur de luminance. Nous pouvons maintenant tenir qu'une image murale lumineuse avec de telles qualités régulières a un facteur Gain de 1,0 dans toutes les directions.
L'Indicatrice du facteur de luminance illustre le comportement de rayonnement d'une image murale lumineuse. Pour une surface (standard blanc) qui sable parfaitement et qui réfléchit parfaitement la lumière, c'est un demi-cercle qui symbolise le facteur de densité briller 1 dans toutes les directions.
Maintenant, on se demande bien sûr comment a l'air une telle Indicatrice pour un mur d'image juste? L'image suivante montre un exemple pour un type de mur d'image D. le demi-cercle noir montre comme référence l'indicatrice pour notre surface parfaitement diffuse et réfléchie de l'image précédente. Le facteur Gain correspondant est &betaW = 1. La demie ellipse rouge indique l'Indicatrice du facteur de luminance lumineuse réelle pour ce mur d'image. Qu'il soit remarqué de nouveau, qu'il ne s'agit pas d'une ellipse mais d'un ellipsoïde; on reçoit ceci, lorsqu'on tourne l'ellipse représentée avec la bordure rouge autour de l'axe optique.
Si nous comparons l'ellipse rouge avec le demi-cercle noir, nous lisons, que cette écran est éfléchit plus fortement dans la direction des murs d'image normaux qu'en direction du bord. Le facteur Gain est alors perpendiculaire avec environ1,2. Par contre, nous lisons pour le facteur Gain vertical à la normale une valeur de 0,8 seulement. Et dans un angle d'environ 60° à l'axe optique, l'ellipse rouge se coupe avec le demi-cercle noir; le facteur Gain est de 1,0. On pourrait alors décrire le comportement d'un tel mur d'image ainsi: Celui qui est assis directement devant cela, reçoit assez de lumière; celui qui est assis un peu en biais à cela, éprouve des conditions de lumière normales; celui qui regarde tout à fait latéralement sur le mur d'image, reconnaît toujours l'image. Qui a la meilleure place dans la pièce, cela dépend de la luminosité du projecteur et de la luminosité de la pièce.
Particulièrement lors de la contemplation de la deuxième image, tout le monde devient clair ce que l'on entend par le facteur de luminance. Et - c'est très important- il devient aussi clair que l'on ne peut pas décrire le comportement de rayonnement d'un mur d'image avec un seul facteur, car un tel facteur Gain n'est valable que pour une direction tout à fait précise. Pour décrire complètement le comportement de réflexion d'un écran, un fabricant devrait indiquer le facteur Gain pour différents angles de contemplation ou joindre simplement une image de l'indicatrice du facteur de luminance. Ce point est si important pour moi, que je le met nouvellement en valeur:
Le facteur Gain donne le comportement de réflexion d'un mur d'image dans une direction précise. Pour décrire le comportement de rayonnement complet d'un écran, on a besoin soit d'un tableau avec les facteurs Gain à certains angles, soit d'une exemplification graphique sous forme d'un indicatrice de facteur de luminance.
Qu'est-ce qui fait un sens en vu de cela, si un fabricant décrit un mur de photo d'identité précis avec un facteur Gain de 1,2? Selon de ce qu'il est dit en haut, il est toutefois juste que cette valeur n'est valable que pour une direction précise pour les murs d'image normaux mais de cette valeur, mais à partir de cette valeur en direction des normaux, le comportement de réflexion approximatif se laisse dériver pour les directions restantes selon l'image ci-dessus.
Mesurage du facteur de luminance
Après que nous avons commencé à savoir ce qui est un facteur de luminance et à partir de quelles deux grandeurs (luminances lumineuses) il est calculé, il se pose la question de mesurage du facteur Gain pour un écran. Selon la définition du facteur Gain, cela s'écoute très simplement: Nous nous achetons un appareil de mesure de densité de lumière, nous illuminons un morceau de l'écran, nous remplaçons ensuite le morceau de mur de photo d'identité à travers un mur de norme, nous mesurons ensuite de nouveau et nous formons le quotient.
Mais la chose n'est pas si simple. Nous avons d'abord besoin d'une source lumineuse adéquate et pour cela il ne suffit pas n'importe quelle lampe mais elle doit produire une lumière de normes A selon DIN 5033-7. Une telle source lumineuse se laisse acquérir exactement comme un appareil de mesure de densité de lumière dans le commerce spécial. Le véritable problème est cependant d'obtenir une surface de référence parfaitement diffuse et réfléchissante, car il n'y en a pas quelque chose comme ça du tout. Au lieu de cela, il sera utilisé une normale de réflexion. Il s'agit ici d'un petit morceau de mur d'image qui est certes, ni parfaitement diffus ni réfléchissant
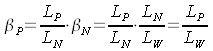 mais dont les qualités sont connues. En d'autres termes, chez une telle normale de réflexion, l'indicatrice correspondant est contenu comme tableau ou graphique; nous connaissons alors le facteur de luminance correspondant βN, à chaque angle de contemplation, qui forme le quotient de la luminance lumineuse de la normale de réflexion et la luminance lumineuse de la référence blanche. Nous exécutons maintenant notre mesure de luminance une fois avec l'essai de mur d'image (notre véritable écran) LP et une fois avec la normale de réflexion de travail LN, nous recevons ainsi notre facteur Gain &betaP selon la formule ci-dessus. Même ici il soit évoqué, que nous devons mesurer le facteur de luminance et le calculer séparément pour chaque angle de contemplation; nous recevons alors βP(ε), où ε est l'angle de contemplation relatif à la normale du mur d'image. Nous tenons les points culminants de ce chapitre dans un cadre:
mais dont les qualités sont connues. En d'autres termes, chez une telle normale de réflexion, l'indicatrice correspondant est contenu comme tableau ou graphique; nous connaissons alors le facteur de luminance correspondant βN, à chaque angle de contemplation, qui forme le quotient de la luminance lumineuse de la normale de réflexion et la luminance lumineuse de la référence blanche. Nous exécutons maintenant notre mesure de luminance une fois avec l'essai de mur d'image (notre véritable écran) LP et une fois avec la normale de réflexion de travail LN, nous recevons ainsi notre facteur Gain &betaP selon la formule ci-dessus. Même ici il soit évoqué, que nous devons mesurer le facteur de luminance et le calculer séparément pour chaque angle de contemplation; nous recevons alors βP(ε), où ε est l'angle de contemplation relatif à la normale du mur d'image. Nous tenons les points culminants de ce chapitre dans un cadre:
Pour mesurer le facteur de luminance βP(ε) on a besoin d'une source lumineuse de norme, d'un appareil de mesure de luminance lumineuse et une normale de réflexion de travail avec des qualités de réflexion avouées βN(ε). Pour chaque direction de contemplation e le mesurage doit être effectué séparément.
En conclusion, on remarque encore que ce processus de mesurage décrit relativement simple en haut est compliqué et d'envergure. Et il n'y a pas aucune normale de réflexion de travail qui conserve constamment ses qualités lumineuses; par conséquent, il arrive, qu'on doit calibrer la normale de réflexion de travail avec celles de réflexion justes.
Représentation du facteur de luminance à travers les courbes de distribution
Nous avons appris dans le chapitre précédent, qu'on peut mesurer le facteur de luminance βP(ε) que pour un angle de contemplation β tout à fait précis. Pour pouvoir faire une déposition solide sur le comportement de rayonnement d'un mur de photo d'identité, on a alors besoin de plusieurs tests uniques avec des angles de contemplation différents.
| Angle de contemplation |
Facteur de luminance |
| 0° |
1,4 |
| ± 20° |
1,2 |
| ± 40° |
1,05 |
| ± 60° |
0,8 |
Si on compose un tel rang de mesure sous forme de tableau dans lequel le facteur de luminance respectif est indiqué pour différents angles de contemplation, ainsi on peut simplement se procurer un aperçu sur le comportement de réflexion du mur de photo d'identité. On peut évaluer des valeurs qui n'arrivent pas dans le tableau à travers l'interpolation. Pour se procurer un aperçu sur le comportement de rayonnement de l'écran et pouvoir surtout comparer les différents murs de photo d'identité, un tel tableau de facteur Gain est cependant moins adéquat. Dans ce cas, il se recommande une exemplification graphique du comportement de réflexion.
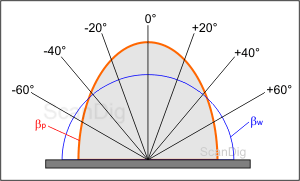
Il y a deux représentations graphiques courantes pour le facteur de luminance: L'utilisation de coordonnées cartésiennes ou l'utilisation de coordonnées polaires. Nous commençons par les courbes de distribution sous forme de coordonnées polaires car nous les avons déjà connus dans l'avant-dernier chapitre. L'image à côté visualise formellement le comportement de réflexion d'un écran. A partir des normales de mur d'image (ligne de 0°), il sera noté des lignes dans des angles réguliers (ici 20°). Ces lignes signifient respectivement une direction de contemplation tout à fait précise. La courbe bleue de référence blanche sert comme une courbe de référence avec un facteur Gain constant de 1. Sur les lignes d'angle respectives, nous appliquons les valeurs mesurées pour le facteur de luminance et nous lions ces points avec la courbe rouge, qui visualise finalement le comportement de réflexion du mur d'image pour l'angle d'incidence de lumière de 0°.
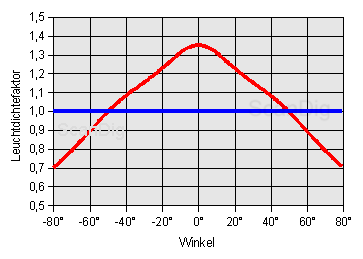
Une représentation graphique alternative de la courbe de distribution de facteur de luminance se produit avec des coordonnées cartésiennes. L'image à côté montre exactement le même contenu que l'image de coordonnées polaires ci-dessus. Ici, nous appliquons comme dans un diagramme les différents angles de contemplation sur l'axe des x et sur l'axe des y le facteur de luminance correspondant. Notre courbe bleue de référence blanche avec un facteur Gain constant de 1 devient une droite dans le diagramme et notre courbe de distribution pour l'écran métré devient une colline de montagne symétrique. Cette forme de représentation a les avantages que nous pouvons lire les valeurs numériques directement du diagramme et que nous reconnaissons clairement la chute de luminance dans le domaine du maximum.
Quelle forme de représentation de la courbe de distribution sera bien éprouvée, dépend pourtant de quoi on en aura besoin. Celui qui voudrait se procurer un aperçu grossier sur le comportement de réflexion d'un mur de photo d'identité, est mieux servi avec la représentation métaphorique dans des coordonnées polaires; Celui qui a besoin par contre de valeurs numériques concrètes pour l'interprétation d'une pièce de présentation professionnelle, aura besoin de la représentation cartésienne.
Je voudrais en conclusion souligner, que non seulement le tableau d'angle de contemplation et son facteur de Gain correspondant, mais aussi la visualisation dans des coordonnées polaires ou des coordonnées cartésiennes ont le même contenu physique.
Retour vers la table de matiére Ecrans de Projection
|